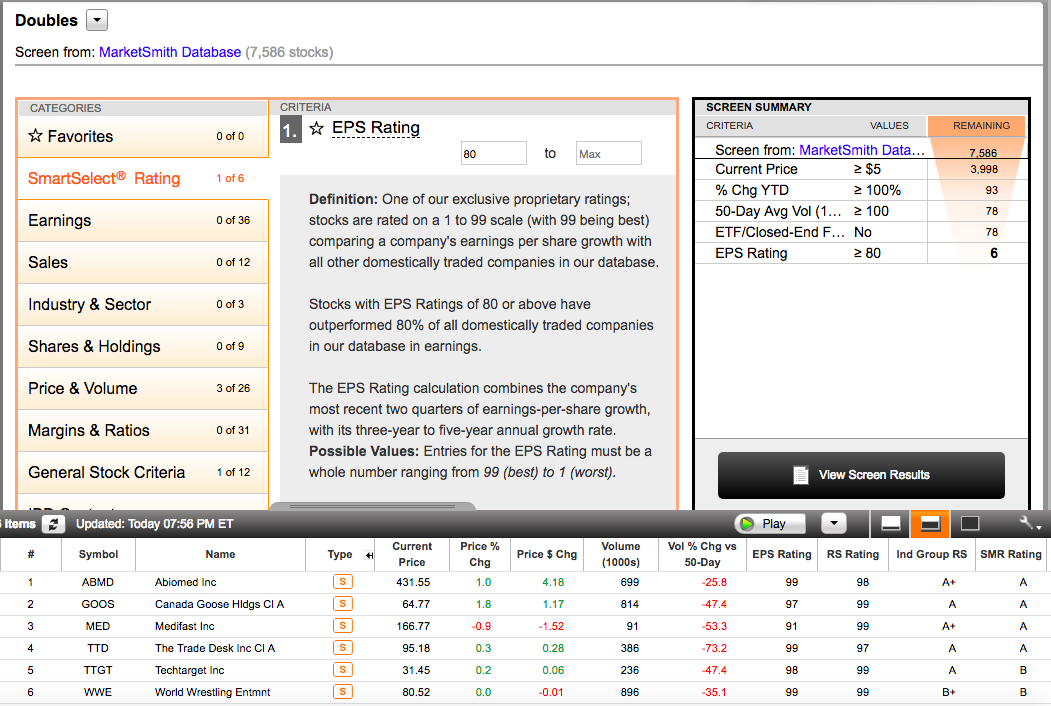
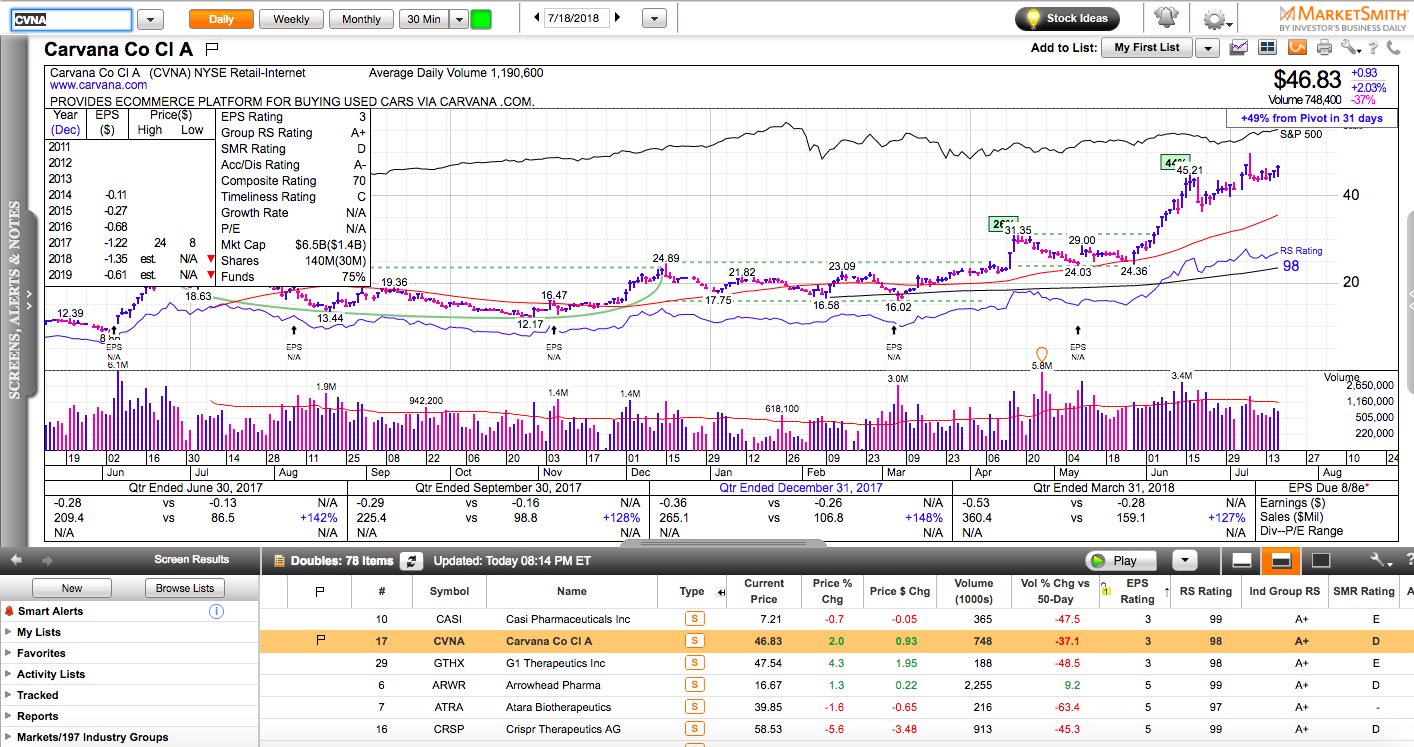
Charts in this post are powered by MarketSmith.
Google is trading at new all-time highs after hours after crushing earnings estimates and now it’s only 15% away from the one-trillion-dollar mark. A follow-through tomorrow would be a major vote of confidence which will likely spread to the rest of tech stocks.
In the meantime, long-term interest rates are finally rising, which is a big boost for financials. It doesn’t make sense to bet against a market led by both, finance and tech.
Disclaimer: everything on this show is for informational and educational purposes only. The ideas presented are not recommendations to buy or sell stocks. The material presented here might not take into account your specific investment objectives. I may or I may not own some of the securities mentioned. Consult your investment advisor before acting on any of the information provided here.